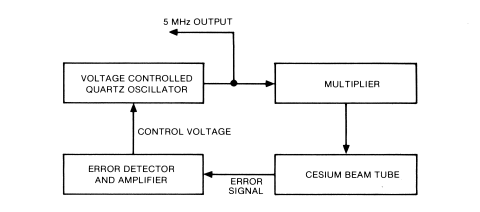
THEORY OF OPERATION

General

Atomic Frequency Standards can be placed into two general categories: active atomic resonators and passive atomic resonators. The active resonators are masers which derive their output signal from the stimulated emission of microwave energy. The hydrogen maser is an active resonator.

The passive atomic resonator serves as an atomic frequency reference by stabilizing a quartz oscillator in a feedback control circuit. A microwave signal derived from the quartz oscillator drives the atomic resonator and induces transitions between desired atomic states in the resonator. The rubidium optical absorption cell and the cesium beam tube are passive atomic resonators.

The 5062C Cesium Beam Frequency Reference (CBFR) can be simply described as a servo-controlled precision quartz oscillator referenced to a passive atomic resonator, the cesium beam tube. Figure 4 shows a simplified block diagram of the 5062C CBFR.

Figure 4. Simplified Block Diagram of 5062C

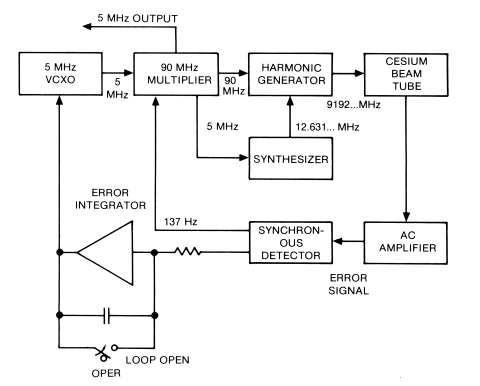
The 5062C makes use of the passive atomic resonance effect in cesium. In order to excite this resonance a frequency equal to the resonant frequency of cesium (with the magnetic field used in the 5062C this frequency is 9,192,631,774.3133 Hz) is applied to the microwave cavity of the cesium beam tube.

The excitation signal is obtained by multiplying the output of a quartz oscillator to the appropriate frequency. Since the quartz oscillator has excellent phase noise characteristics, it may be multiplied into the microwave region without serious degradation of signal quality.

If the frequency of the signal applied to the cesium beam tube is not correct, an error signal is generated and is present at the output of the beam tube. This error signal is amplified, detected, and fed back to the voltage controlled quartz oscillator to correct its frequency. Thus, when the quartz oscillator tries to drift, an error signal is produced which corrects the quartz oscillator and keeps its frequency at an exact submultiple of the atomic resonance frequency. If the loop gain of this servo system is high, the accuracy of the output frequency becomes that of the cesium beam tube. The short term stability of the output is determined by noise coming from the cesium beam tube, short term stability of the quartz oscillator, and the servo loop time constant.

5062C Operation

Let us now look at the operation of the 5062C in a little more detail before examining the cesium beam tube. Figure 5 shows the block diagram of the 5062C.

Figure 5. 5062C Block Diagram

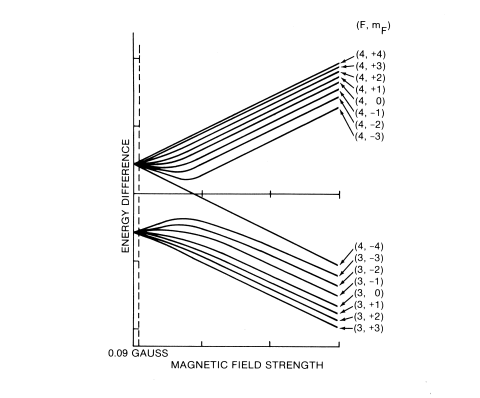
As was mentioned earlier, the output of the 5062C is derived from a highly stable 5 MHz voltage controlled crystal oscillator (VCXO) whose frequency is locked to the invariant resonance of the cesium atom undergoing a change of atomic state in the beam tube. The VCXO is a rugged, stable 5 MHz oven oscillator capable of excellent performance by itself. It has excellent spectral purity and short term stability (1 x 10^-11 rms for a one second averaging time).

The 5 MHz signal is routed to the 90 MHz multiplier where it is relayed to a buffer amplifier and from there is provided as isolated outputs on front and rear panels of the 5062C. The 5 MHz signal is also relayed to the Synthesizer which synthesizes 12.6317743133 MHz. Inside the 90 MHz Multiplier the 5 MHz signal is first modulated at a 137 Hz rate and then multiplied by 18 to produce 90 MHz.

The Harmonic Generator multiplies the 90 MHz by 102 to obtain 9180 MHz. The 9180 MHz is then combined with the 12.6317743133 MHz to provide the cesium resonant frequency (in a magnetic field of about 0.09 gauss), 9,192,631,774.3133 Hz which is injected into the microwave cavity of the cesium beam tube.

The cesium beam tube produces an output current, as discussed earlier, consisting of an average dc value and ac components at 137 Hz and harmonics. If the VCXO frequency is exactly 5 MHz, the beam tube input frequency will be exactly 9,192,631,774.3133 Hz and the output current is modulated only at even harmonics, primarily the second harmonic, 274 Hz. If the VCXO differs from 5 MHz the output current will have a 137 Hz component whose amplitude indicates the difference between the beam tube input frequency and the cesium resonance frequency, and whose phase indicates the sign of the difference.

The output current is amplified and synchronously detected using as a reference the self-contained 137 Hz oscillator which generated the modulation. The synchronous detector and an integrator produce an error signal that is applied to the VCXO Electronic Frequency Control (EFC) input to adjust the 5 MHz oscillator to exactly 5 MHz. Thus, the VCXO is controlled through the servo loop containing the beam tube to produce a very stable 5 MHz output signal.

Cesium Beam Tube

Physics of the Cesium Beam Tube.  From the block diagram description of the 5062C we might consider the cesium beam tube to be acting as though it were a frequency discriminator (or a bandpass filter) with a very narrow response curve in the vicinity of the transition frequency, f₀. How discriminator action comes about will be apparent after the physical principles behind the cesium beam resonator have been examined.

Atoms can occupy only certain discrete energy levels and transitions between these energy levels occur by "jumps" predicted by quantum mechanical rules. The difference in energy (ΔE) between two states is related to the transition frequency f by ΔE = hf, where h is Planck's constant. It is upon this frequency f, corresponding to a transition between two atomic states separated in energy by ΔE, that atomic frequency standards are based. If we can somehow select atoms according to energy level, excite these atoms with a frequency which is swept through the transition frequency under just the proper conditions, and detect those atoms which have undergone the predicted transition, we then have a means of access from the external world to the atomic frequency. A maximum number of atoms will be detected when the frequency has exactly the value which optimizes the transition probability.

Cesium atoms can be selected for energy state by application of a magnetic field gradient, and cesium has other qualities also appropriate to its use in a frequency standard. Cesium, like hydrogen and rubidium, has a single valence electron. Between this electron and the nucleus there are magnetic interactions; we will focus our attention on interactions between the valence electron's spin dipole moment and that of the nucleus, with the atom in its lowest energy state, the electronic ground state. The electron spin has two possible orientations (quantum mechanical rules) and two energy levels correspond to these. It is convenient to think in terms of parallel and anti-parallel orientations for the two spins; the corresponding energy states are designated by the quantum numbers F = 3 and F = 4. To summarize, the cesium atom's ground state is split by magnetic interactions into two energy levels and the separation between these levels is referred to as the hyperfine structure.

Upon application of an external magnetic field, the two hyperfine structure levels each split into a number of distinct levels. These are the Zeeman hyperfine levels designated in quantum notation by m numbers, corresponding to allowed orientations of the atom with respect to the external magnetic field.

Figure 6 shows the energy level diagram of cesium as a function of the applied magnetic field. The hyperfine transition of interest is the one separating the states F = 4, m_f = 0 (4,0) and F = 3, m_f = 0 (3,0) at low magnetic fields. This transition is well suited to use in a frequency standard because it is very nearly independent of the external magnetic field, whereas for other transitions, there is a linear dependence upon field. Reference will be made to this later, in the discussion of the "C" field within the cesium beam tube.

An applied radiation field of frequency appropriate to the transition. under discussion induces atoms in the F = 4 state to emit a quantum of energy, and those in the F = 3 state to absorb a quantum of energy; they are reversed in their magnetic moments following such transition, and are said to have flopped.

Figure 6. Energy Level Diagram for Cesium 133

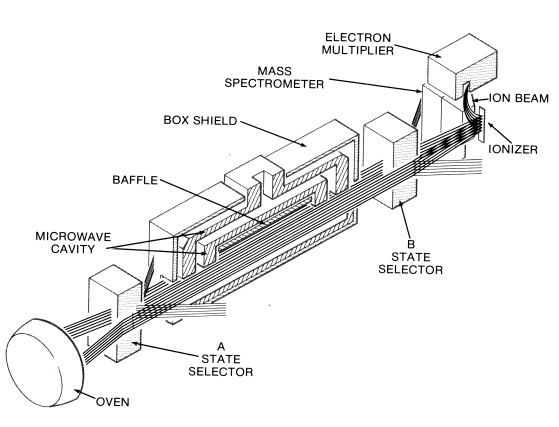
Cesium Beam Tube Operation.  Figure 7 shows a schematic of the cesium beam tube.

Figure 7. Cesium Beam Tube Schematic

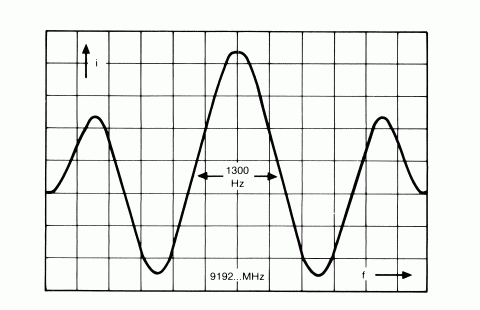
Cesium atoms effuse from the oven source and are formed into twelve ribbon-like beams by a collimator. The beams pass through the inhomogeneous magnetic field of the first state selector magnet, the "A" magnet. The force experienced by a particular atom depends upon its effective magnetic moment, hence upon its energy state, and also upon the gradient of the field; thus, atoms (all of the F = 3 as well as the 4, -4 atoms) are selectively deflected into the interaction cavity. Two fields are present in this cavity, the "C" field and the microwave field resulting from multiplication and synthesis from the quartz oscillator. The presence of the C field, a steady-state, low level field, causes the desired separation to exist in the cesium atom's energy levels. The magnetic component of the injected microwave field interacts with the atoms. If the frequency is at the transition frequency, 9,192,631,774.3133 Hz then atoms flop to the other transition energy state. Since their effective magnetic moment is 1hereby reversed in its direction, a second state selector magnet, the "B" magnet, can selectively deflect flopped atoms to the detector. This detector, a hot wire ionizer ionizes the cesium atoms with nearly 100 percent efficiency. An electric field directs the cesium ions into a mass spectrometer which acts to select cesium ions by directing only cesium ions to the first dynode of an electron multiplier where the signal is amplified by about 10⁵.

The shorter microwave interaction cavity of a small beam tube with a single beam output would be noisier than the beam tubes for the 5061A. To improve the performance, twelve beams of cesium are used in the small tube instead of one or two as in the 5061A beam tubes. This provides a signal to noise ratio which allows the beam tube to operate with performance approaching that of the standard 5061A beam tube with a single cesium beam.

An additional benefit of the smaller beam tube design is a reduced sensitivity to acceleration and vibration due to the utilization of multiple beams.

Beam Tube Output Current.  Beam current goes through a maximum when the frequency of the applied radiation field sweeps through the resonant frequency of the cesium transition. Figure 8 shows this beam current peak; the side lobes are a consequence of the Ramsey type of excitation, that is, in two separated regions. Width of the central peak and the distance between peaks are functions of the length of the interaction cavity and of the average velocity of the atoms.

Figure 8. Beam Tube Output Current

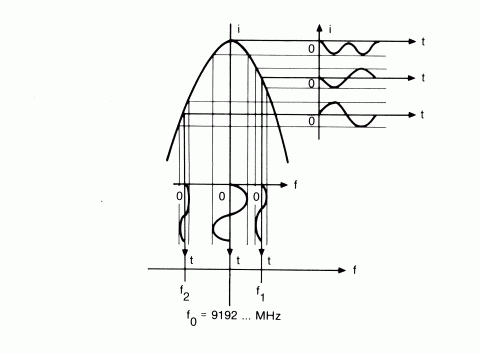
All of the above interactions simply set up the cesium atoms to function as a frequency discriminator. During normal operation of the 5062C, the input microwave frequency will lie upon the central peak. Recall that the applied microwave frequency is phase modulated at 137 Hz. Figure 9 shows one cycle of the resulting variation for three values of the carrier. With f centered at f₀ the transition frequency, the output beam current varies at twice the input frequency. If the carrier lies above f₀ as shown by the plot labeled f, output current varies at the same rate as the modulation but has been shifted by 180° with respect to it; when the carrier lies below f₀ (case f₂) no phase shift occurs.

To summarize this information: when the applied microwave signal is matched to the cesium resonant frequency, only the second harmonic component of the modulation signal appears in the beam current output. When the applied signal lies above or below this desired value, beam current output contains both fundamental and second harmonic modulation components. These components are used by the instrument to evaluate the correction necessary to tune the crystal oscillator to zero frequency error.

Figure 9. Discriminator Action of the Cesium Beam Resonance

Should incorrect adjustment of the 5062C cause the beam tube to be centered on a side lobe rather than on the central peak, logic circuits sense the presence of quadrature fundamental and signal the operator via the ALARM light on the 5062C's front panel.

C-Field.  Cesium-atom transitions are possible between any pair of sub-levels shown in Figure 10 for which the second quantum number either does not change or changes by ±1 (Δm = 0 or 1). To avoid the errors caused by line asymmetry when operating in a zero magnetic field, a small magnetic field is applied to the microwave cavity. By applying a small field of about 0.09 gauss, the Δm_f = 0 transitions are separated by about 70 kHz in frequency so that any residual overlap causes negligible error. This field is termed the C-Field.

Figure 10. Full Microwave Spectrum for the Cesium Beam Tube

The C-Field can be used to make small frequency adjustments of the instrument to bring its frequency closer to that of a desired reference frequency. The dependence of the frequency on magnetic field is given by f = 9192631770 + 8.7026x10^-10f_z², where f and f_z are in Hertz. The Zeeman frequency, f_z, is the average difference in frequency between the 3,0 to 4,0 transition and the adjacent field-dependent transitions. f_z has a linear dependence on magnetic field.

Visualize the effect on this spectrum if the C-Field were varied. The 0,0 transition would remain in virtually the same place, while the field dependent transitions would be shifted further apart as C-Field increased. This separation of the energy dependent transitions, which is a known and sensitive function of the C-Field, is used to set the C-Field and to align the 5062C. It may be noted that resolution of the C-Field control is two parts in 10¹² per minor division.

It is convenient to produce the frequencies used to excite the field dependent transitions by modulating the output of the 5062C's harmonic generator such that sidebands lie at the desired frequencies. The 5062C has an input jack (the "Zeeman Mod Freq" jack) for easy connection to a HP 204C Audio Oscillator (or equivalent). An error of one percent in the modulating frequency, will cause an error of only 9.4 x 10^-12 in the 5 MHz output frequency.

After the turn-on procedure, which uses the cesium beam resonator to check on its own performance, output frequency is known to the accuracy specified without the need for reference to another standard. No secondary standard such as rubidium or quartz is capable of this intrinsic accuracy and reproducibility.